What’s the point?

As explained here, economics assumes we are all sociopaths (purely self-focused). So of course, the prisoners in their famous Prisoners’ Dilemma Game (PDG) are also sociopaths. Standard game theory claims this means they never cooperate — even if they know they’re going to play the game over and over.

But even with this strong assumption (that both are sociopaths), this conclusion is not valid (See Kreps, Milgrom, Roberts & Wilson, 1982). Sociopaths are only guaranteed to act like (obvious) sociopaths when playing with other known sociopaths. If there are honorable players around, sociopaths may find it selfishly advantageous to mimic them.

What I will show here is that if both players are sociopaths (what econs call “rational”), but neither knows what kind of player the other is, the two sociopaths may cooperate in the first stage of a two-stage PDG. Since non-sociopaths are quite common, this is a good step toward showing how unscientific standard game theory is.

The (1-stage) PDG used in this proof

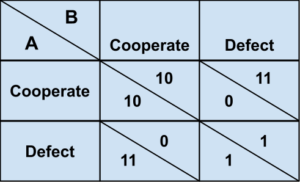
If player A cooperates, B gets 10 for cooperation but 11 for defection. If A defects, B gets 1 for cooperation and 2 for defection. So no matter what A does, player B is better off if B defects. The same is, of course, true for A. So both defect.

Since both would be worse off if they changed their strategy (given the other’s strategy) this is a Nash equilibrium. Standard game theory predicts this will happen.

The Supergame

If the same two prisoners play this game several times in a row, that’s a “supergame.” The final stage of such a supergame is simply a PDG, so we know both players will defect in the final game. Knowing this, they have no reason to cooperate in the 2nd-to-last stage game, so they defect in this PDG as well. And by backward induction, they defect in every stage of the supergame.

These predictions depend (at least) on A and B being sociopaths (own-payoff maximizes). But we will soon see that is not enough.

Applying Science to the Prisoner’s Dilemma

Suppose half of all prisoners are sociopaths. We know there is “honor among thieves,” so let us assume the other half is honorable. Their utility function values both own-payoffs and honor (cooperating with their fellow prisoner). Further, assume that $1 is not enough to compensate for their loss of honor caused by defection when the other cooperates. Hence honorable prisoners will cooperate until double-crossed.

Assume honorable players play tit-for-tat: First, they play “cooperate,” and then they play whatever the other player played last time.

Now here’s the puzzle

Prove that both players will cooperate in the first stage if:

• the same two players play a two-stage PD supergame: PD1 then PD2
• both are sociopaths
• both think the other player has a 50/50 chance of being honorable

Proof:

1. If player A plays c (cooperate) in PD1 what happens in PD2?
   1. Sociopath A will play d (defect) in PD2.
   2. If B is honorable, B will play c in PD2 and A gets $11
   3. If B is sociopathic, B will play d in PD2 and A gets $1
   4. With a 50% of each, If A plays c then A expects $6 in PD2.
2. If player A plays d (defect) in PD1 what happens in PD2?
   1. Sociopath A will play d (defect) in PD2.
   2. Whether honorable or not, B will play d and A will get $1.
   3. If A plays d in PD1, then A expects $1 in PD2.
3. The same is true for Player B
4. So in PD1 the players will get the payoffs shown in the table above plus an extra (expected) $6 if they are playing cooperate and an extra $1 if they are playing defect.
5. This gives the following expected total super-game payoff table as it is viewed in PD1

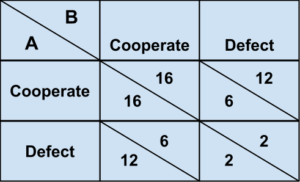
• The PD1 game has a cooperative Nash Equilibrium because, if A cooperates, then the best B can do is cooperate (to win 16 instead of 12). And if A defects, the best B can do is cooperate to win 6 instead of 2.
• So both players, although they are sociopaths, will cooperate in PD1, and then of course they will defect in PD2.  QED

---

This way they each earns 10 + 1 = 11 instead of 1 + 1 = 2 as they would if they didn’t cooperate in either game. And this happens only because they both believe the other one might be an honorable (tit-for-tat) player.

This result also means that if they played a 100-stage PD supergame, they would cooperate for the first 99 games and then defect on the final game.

But what would happen if they both knew that the other was a sociopath. That would probably spoil the cooperation in a 2-states PD super game. But if they didn’t know that the other one knew that they were a sociopath, we might still get cooperation if the supergame had three or four stages. I hope to investigate this later.